Neural networks are adaptive learning systems, inspired by the biological neural systems. These may be trained with input-output data or may operate in a self-organizing mode. The basic block in an NN is the mathematical model of a neuron as in Eqn. 1. Three fundamental components of a neuron are the connection links that provide the inputs with weights for = 1,…, , an adder that sums all the weighted inputs to prepare the input to the activation function along with the bias associated with each neuron, and an activation function maps the input to the output of the neuron.
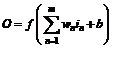
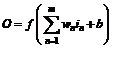
an activation function f is typically a sigmoid function. The scalar parameters of the neuron, the weight and the bias, are adjustable. Single input neuron, multi-input neuron, and multi-input multi-neuron models are shown in Fig. 1.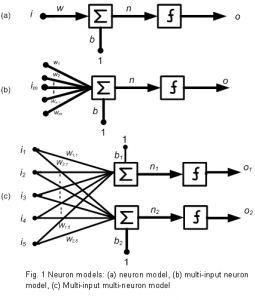
Neuron activation functions
Several activation functions have been used in neural networks. The simplest of all is the linear activation function used as a linear approximators. This function can be uniploar with saturation levels of 0 and 1or bipolar with saturation levels of -1 to +1 as shown in Fig. 2(a). The threshold and signum functions outputs vary abruptly between 0 to +1 and -1 to +1, respectively as shown in Fig. 2(b). These are used in perceptrons for classification problems. The sigmoid and Gaussian activation functions are nonlinear, differentiable, and continuous. These properties extend the application of neural networks from linear analysis to complex and nonlinear analysis applications. The sigmoid functions are a family of S-shaped functions. Logistic function, as shown in Fig. 2(c), is the most widely used sigmoid function andit has lower bound of 0 and upper bound of 1. Another commonly used sigmoid function is the hyperbolic tangent function with lower bound at -1 and upper bound at 1 as shown in Fig. 2(c). In both of these sigmoid functions, for inputs grater than 0, output initially rapidly and later slowly increases. For inputs less than 0, output rapidly decreases and later slowly decreases. Gaussian functions are symmetric bell shaped functions it represents the input with zero mean and standard deviation equals to one. Standard normal curve is the Gaussian function with bounds 0 and 1. It peaks at zero input and is more sensitive around zero input and less or zero sensitive at tails. In Gaussian
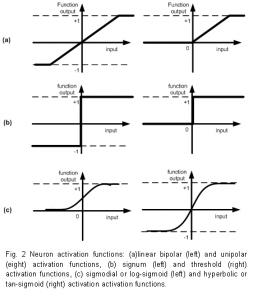

complement, more sensitive at tails and zero at zero input.
Keywords: Neural Network, Neuron Model, Activation Functions, Linear Bipolar, Signum, Sigmodial, Log-sigmoid, Hyperbolic, Tan-sigmoid
Dr. S. Mohan Mahalakshi Naidu
Associate Professor – Electronics & Telecommunication Engineering Department



